Motivation
Support Vector Machine (SVM) is one of the most popular algorithm in machine learning classification tasks whose training data size is reasonable. However, when I was working on machine learning regression tasks using some python libraries, such as scikit, I often saw there is a regressor called Support Vector Regressor (SVR). What the hell is this algorithm? Isn’t support vector machine a classification algorithm? How does it work for regression problems?
Support Vector Machine
Support vector regression has some subtle difference to support vector machine regarding their physical meanings despite the fact that their formula are quite similar. Let us take a glance at support vector machine first. Basically, for a linearly separable classification task, support vector machine finds a line or hyperplane \( w^Tx+b = 0 \) that maximize the “margin” from the classifier to the closest data. Every thing seems to be “right”. Neigher too big, nor too small. It is “the Goldilocks principle” from the fairy tale “the Goldilocks and the three bears”.

To express the whole idea using formula, we have an optimization problem:
\( \min \frac{1}{2} \|w\|^2 \) subject to \( y^{(i)}(w^Tx^{(i)}+b)\ge1 \) for all \(i = 1,2, …, n \)
Here, the “margin” from the classifier \( w^Tx+b = 0 \) to the closest data point is \( \frac{1}{\|w\|^2} \) where the closest data point \(x^{(c)}\) has \( y^{(c)}(w^Tx^{(c)}+b)=1 \). Minimizing \( \frac{1}{2} \|w\|^2 \) is actually maximizing the “margin”.
The red line H3 is the support vector machine classifier that maximize the “margin”. It should be noted that the constrain garantees that the classifier classify the data points correctly with the miximized “margin”.
For more details of support vector machine, how to solve the above formulated optimization problem, non-linearly separable classification problem, and the kernel trick, you may read the support vector machine course material from Andrew Ng’s Stanford CS229 Machine Learning course.
Support Vector Regression
The simplest version of support vector regression is an similar optimization problem formulated below:
\( \min \frac{1}{2} \|w\|^2 \) subject to \( |y^{(i)} - (w^Tx^{(i)}+b)| \le \epsilon \) for all \(i = 1,2, …, n \)
So, how do we understand this?
There is no “maximization of margin”, and the margin \( \frac{1}{\|w\|^2} \) in support vector classification does not have any physical meaning in support vector regression. The purpose of the minimization of \( \frac{1}{2} \|w\|^2 \) is only to have small weights preventing overfitting. With a good \( \epsilon \), the regressor will go through all the data points with error no more than \( \epsilon \). However, if \( \epsilon \) is not optimal, say, too large. One could anticipate that the constrains are basically doing no job, resulting all the weights to be zero. By choosing different \( \epsilon \), you may or may not get a regressor to satisfy all the data points. Because of this instability, there are no implementation of this form of the algorithm in the scikit. To allow some deviation, one may expand this optimization formula further. Here are some handouts (material 1, material 2) regarding support vector regression, which I am not going to further discuss here. Because the purpose of this blog article is only to compare the intuition difference between support vector machine and support vector regression. My personal understanding is that their name is similar just because they happen to have a similar optimization fomular, and optimization method (check the reading materials). However, there is no too much internal logic connection between them.
There are more parameters in the model. Sometimes, the parameters are very critical for fitting the data to the model, compared to some simple models. Here I generated some data, used ordinary linear regression and support vector regressor to fit the models, and compared their performance. You may see that support vector regressor is very sensitive to model hyperparamters.
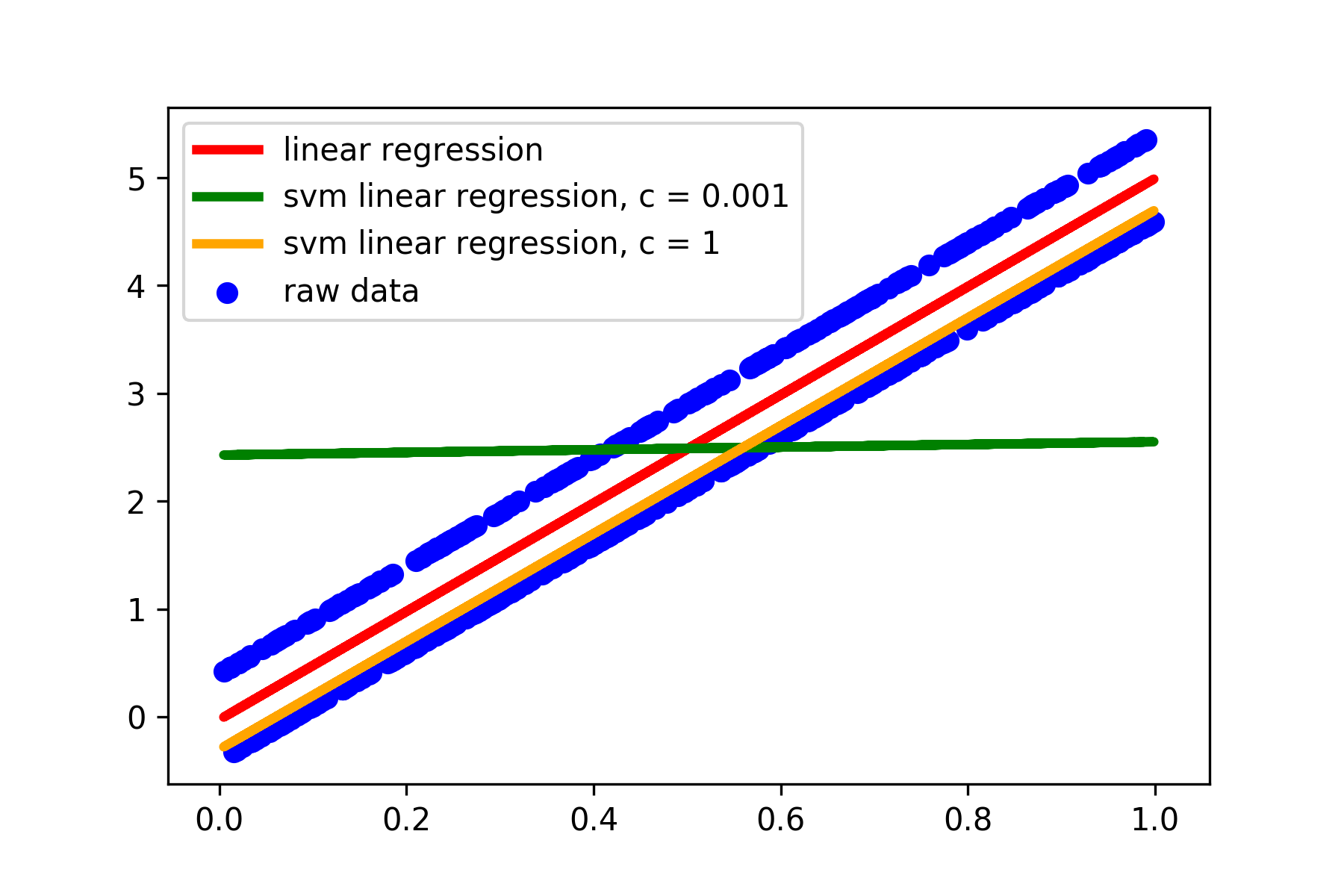
I only changed the C value in the model in the default linear support vector regressor (It does not allow to have C=0!). However, the performance is still far from satisfying compared to the ordinary simple linear regression model. One have to further optimize the \( \epsilon \) value in order to achieve good performance (data not shown). The code for the above support vector regressor model is here.
A good idea to determine the right parameters to use might be doing validation using validation dataset during the model optimization.

